Accessing Fitted Model Objects • tidyfit

library(dplyr); library(tidyr); library(purrr) # Data wrangling
library(tidyfit) # Auto-ML modeling

The fitted model object is contained in tidyfit.models frame in the model_object column as an R6 class. The tidyFit R6 class contains both the underlying model (...$object) as well as additional information generated during fitting and needed to obtain predictions or coefficients.

Suppose, for instance, we want to visualize the regression tree of the hierarchical features regression for different degrees of shrinkage (see ?hfr::plot.hfr). We begin by loading Boston house price data and fitting a regression for 4 different shrinkage parameters. Note that we do not need to specify a .cv argument, since we are not looking to select the optimal degree of shrinkage:

data <- MASS::Boston
mod_frame <- data %>% 
  regress(medv ~ ., m("hfr", kappa = c(0.25, 0.5, 0.75, 1))) %>% 
  unnest(settings)
mod_frame
#> # A tibble: 4 × 7
#>   model estimator_fct `size (MB)` grid_id  model_object kappa weights
#>   <chr> <chr>               <dbl> <chr>    <list>       <dbl> <list> 
#> 1 hfr   hfr::cv.hfr          1.63 #001|001 <tidyFit>     0.25 <NULL> 
#> 2 hfr   hfr::cv.hfr          1.63 #001|002 <tidyFit>     0.5  <NULL> 
#> 3 hfr   hfr::cv.hfr          1.63 #001|003 <tidyFit>     0.75 <NULL> 
#> 4 hfr   hfr::cv.hfr          1.63 #001|004 <tidyFit>     1    <NULL>

kappa defines the extent of shrinkage, with kappa = 1 equal to an unregularized least squares (OLS) regression, and kappa = 0.25 representing a regression graph that is shrunken to 25% of its original size, with 25% of the effective degrees of freedom. The regression graph is visualized using the plot function.

Let’s examine the first model in the tidyfit.models frame:

mod_frame$model_object[[1]]
#> <tidyFit> object
#>  method: hfr | mode: regression | fitted: yes 
#>  no errors ✔ | no warnings ✔

Accessing the fitted model

We have two options to plot the regression trees. Many generics function directly on the tidyFit class. Therefore, we could simply plot (in this case the unregularized regression graph):

mod_frame %>% 
  filter(kappa == 1) %>% 
  pull(model_object) %>% 
  .[[1]] %>% 
  plot(kappa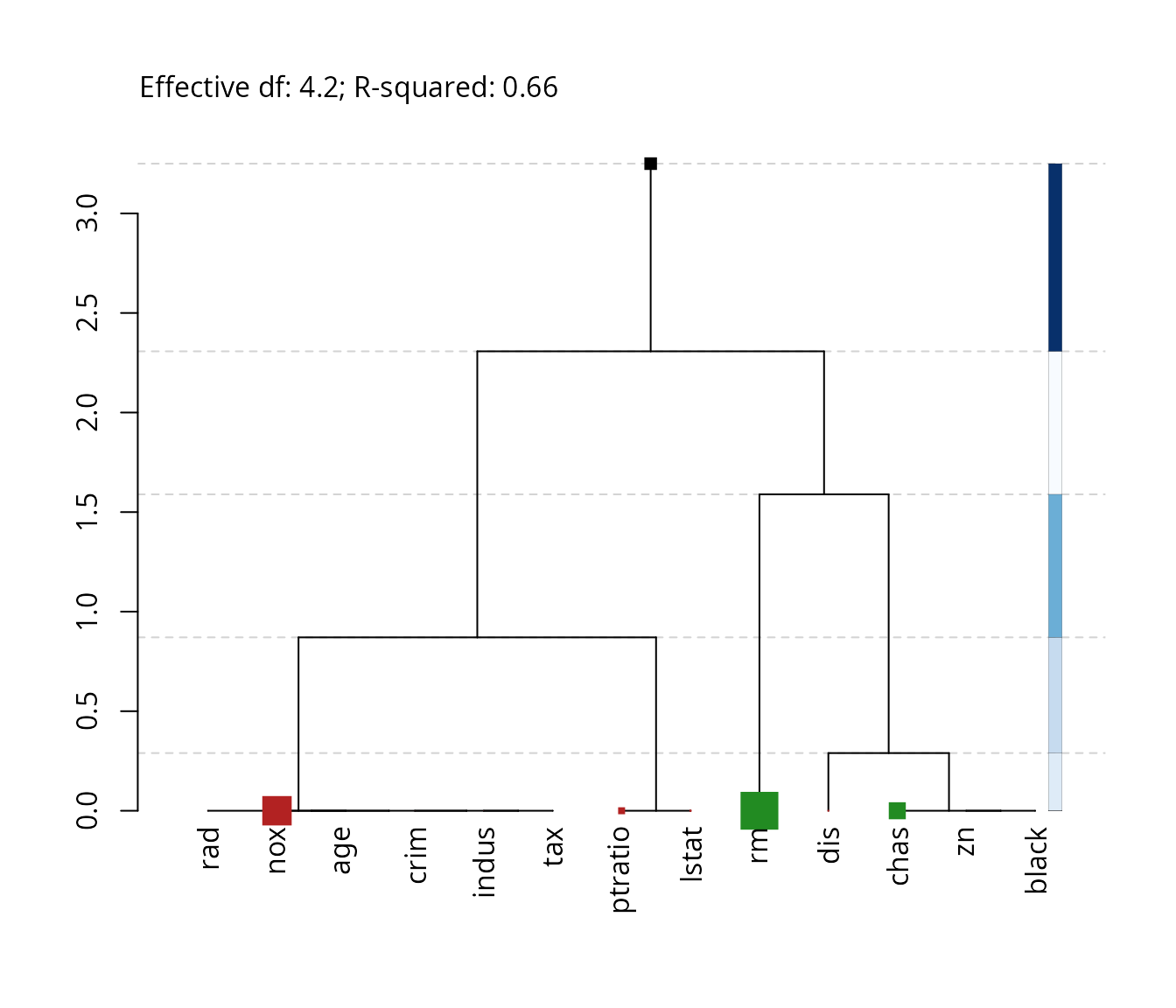 = 1)

The regression graph shows which variables have a similar explanatory effect on the target (variables that are adjacent have a similar effect). The sizes of the leaf-nodes represent the absolute size of the coefficients.

Alternatively, we could access the underlying cv.hfr object using ...$object:

mod_frame <- mod_frame %>% 
  mutate(mod = map(model_object, ~.$object))
mod_frame
#> # A tibble: 4 × 8
#>   model estimator_fct `size (MB)` grid_id  model_object kappa weights
#>   <chr> <chr>               <dbl> <chr>    <list>       <dbl> <list> 
#> 1 hfr   hfr::cv.hfr          1.63 #001|001 <tidyFit>     0.25 <NULL> 
#> 2 hfr   hfr::cv.hfr          1.63 #001|002 <tidyFit>     0.5  <NULL> 
#> 3 hfr   hfr::cv.hfr          1.63 #001|003 <tidyFit>     0.75 <NULL> 
#> 4 hfr   hfr::cv.hfr          1.63 #001|004 <tidyFit>     1    <NULL> 
#> # ℹ 1 more variable: mod <list>

Now there is a column with cv.hfr objects. This is useful, when we want to perform any analysis not directly implemented in the tidyFit generics.

Comparing different regression graphs

Finally, we can use pwalk to compare the different settings in a plot:

# Store current par before editing
old_par <- par()

par(mfrow = c(2, 2))
par(family = "sans", cex = 0.7)
mod_frame %>% 
  arrange(desc(kappa)) %>% 
  select(model_object, kappa) %>% 
  pwalk(~plot(.x, kappa = .y, 
              max_leaf_size = 2, 
              show_details = FALSE))

# Restore old par
par(old_par)

Notice how with each smaller value of kappa the height of the tree shrinks and the model parameters become more similar in size. This is precisely how HFR regularization works: it shrinks the parameters towards group means over groups of similar features as determined by the regression graph.